Теория: 05 Описанный треугольник

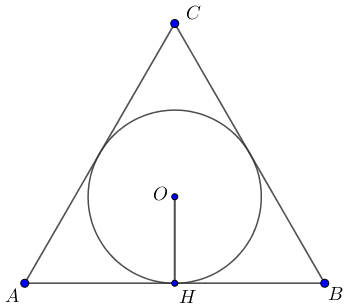
Проведем высоту \(\displaystyle CH\) правильного треугольника \(\displaystyle ABC \small.\) 

Пусть точка \(\displaystyle O\) – центр вписанной окружности.

Центр вписанной в треугольник окружности – точка пересечения биссектрис.

Биссектрисы правильного треугольника являются также высотами.  Значит, точка \(\displaystyle O\) лежит на высоте \(\displaystyle CH \small.\) Поскольку отрезок \(\displaystyle OH\) перпендикулярен основанию треугольника, то он является радиусом окружности.

Так как высота \(\displaystyle CH\) равностороннего треугольника является и его медианой, то 

\(\displaystyle AH=\frac{1}{2} \cdot AB=\frac{\sqrt{3}}{2} \small.\)

Найдем длину отрезка \(\displaystyle CH\) из прямоугольного треугольника \(\displaystyle ACH \small.\) 

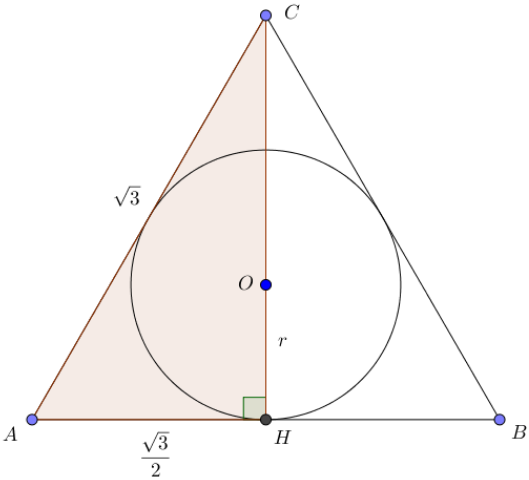По теореме Пифагора \(\displaystyle AC^2=AH^2+CH^2 \small.\) Тогда \(\displaystyle CH^2=AC^2-AH^2 \small,\) \(\displaystyle CH^2=(\sqrt{3})^2-\left( \frac{\sqrt{3}}{2}\right)^2=3-\frac{3}{4}=\frac{9}{4}\small.\) Поскольку длина отрезка положительна, то  \(\displaystyle CH=\frac{3}{2} \small.\)

Высоты правильного треугольника являются также медианами, значит точка \(\displaystyle O\) – точка пересечения медиан.

Тогда точка \(\displaystyle O\) делит медиану \(\displaystyle CH\) в отношении \(\displaystyle 2:1 \small,\) считая от вершины \(\displaystyle C \small.\)

Следовательно, 

\(\displaystyle r=\frac{1}{3} \cdot CH=\frac{1}{3} \cdot \frac{3}{2}=\frac{1}{2}=0{,}5 \small.\)

Ответ: \(\displaystyle 0{,}5 {\small .}\)